EWMA’s are… different

While I was working on reproducing a paper that describes a “reasonable alternative to the W’bal models”¹, I realized that my understanding of the exponentially weighted moving average (EWMA) was not as good as I thought it was, or at least that my “internal model” of what the data would look like was not correctly calibrated with the EWMA that is used in the paper.

Wikipedia’s definition of the EWMA is as follows:

An exponential moving average (EMA), also known as an exponentially weighted moving average (EWMA),[5] is a first-order infinite impulse response filter that applies weighting factors which decrease exponentially. The weighting for each older datum decreases exponentially, never reaching zero. This formulation is according to Hunter (1986).

The version of the EWMA that is used in the paper (equation 3 from the paper) is this:

$$ \text{EWM}_{k,i+1} = \frac{(P_i - \text{EWM}_{k,i}) \cdot (t_{i+1} - t_i)}{\tau_k} + \text{EWM}_{k,i} $$ …with a starting value of 0.

This method corresponds to calculating alpha (the variable that controls the responsiveness of the EWMA) from \(\tau_k\) like this:

$$ \alpha = \frac{1}{1 + \tau_k} $$

In Python/Pandas, this would look something like this:

alpha = 1 / (1 + tau_k)
ewma = power.ewm(alpha=alpha, adjust=False).mean()

…with the difference that the result of this starts at the first value of the input and not at 0 (which makes more sense in this context).

Usually, when talking about moving averages, especially in the context of timeseries data in sports, we talk about the simple moving average (SMA) where all data points in a window of a fixed size are given equal weight to calculate the average.

In Python/Pandas, this would look something like this:

sma = power.rolling(window=window).mean()

My expectation was that the EWMA would be very similar to the SMA when \(\tau_k = \text{window}\), but with a bit of a lag. That was not the case…

Let’s take a look at an simple workout example:

• 10 minutes at 100 Watt.
• 2x6 minutes at 200 Watt, with 6 minutes at 100 Watt in between.

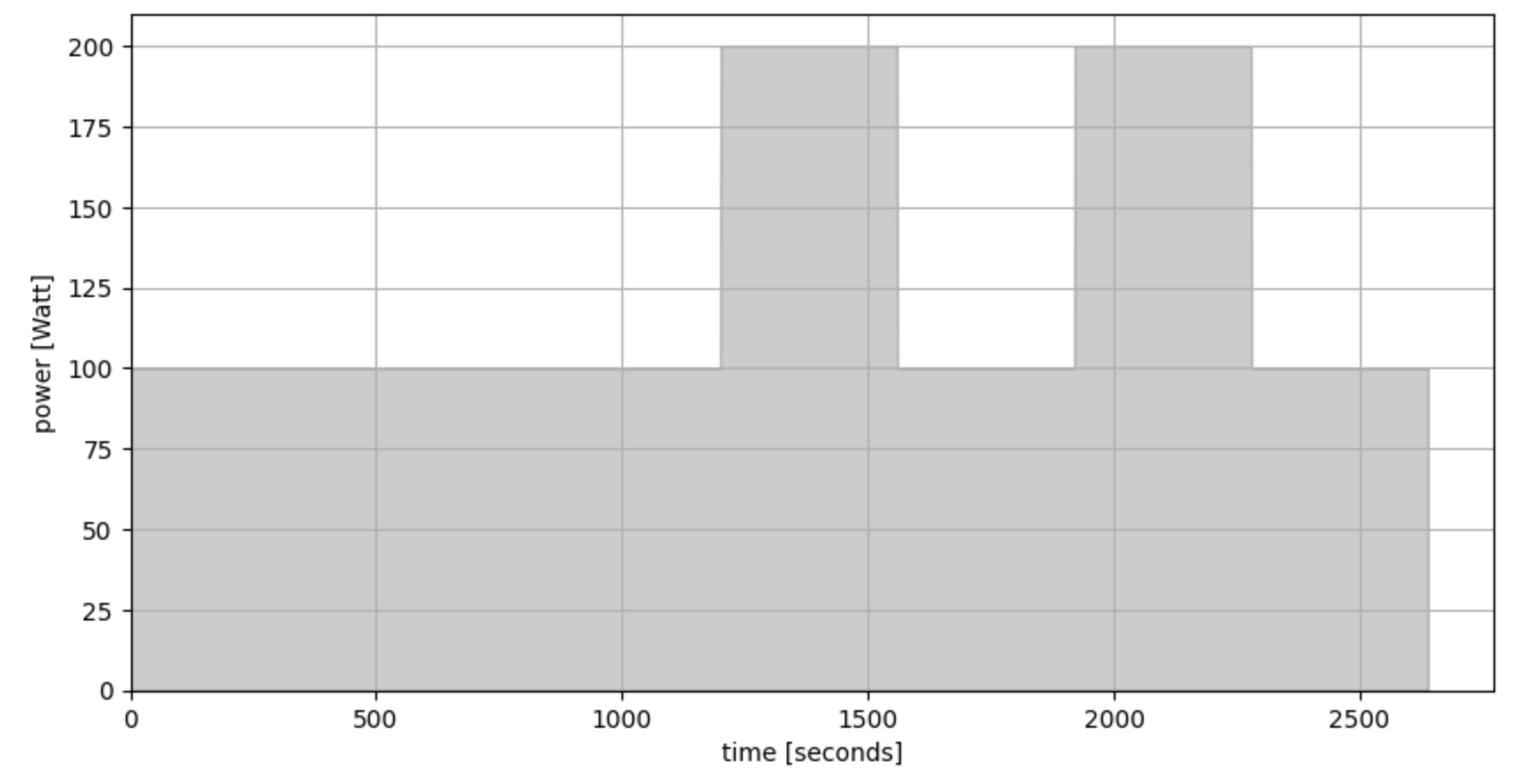
The SMA and EWMA for this activity look like this:

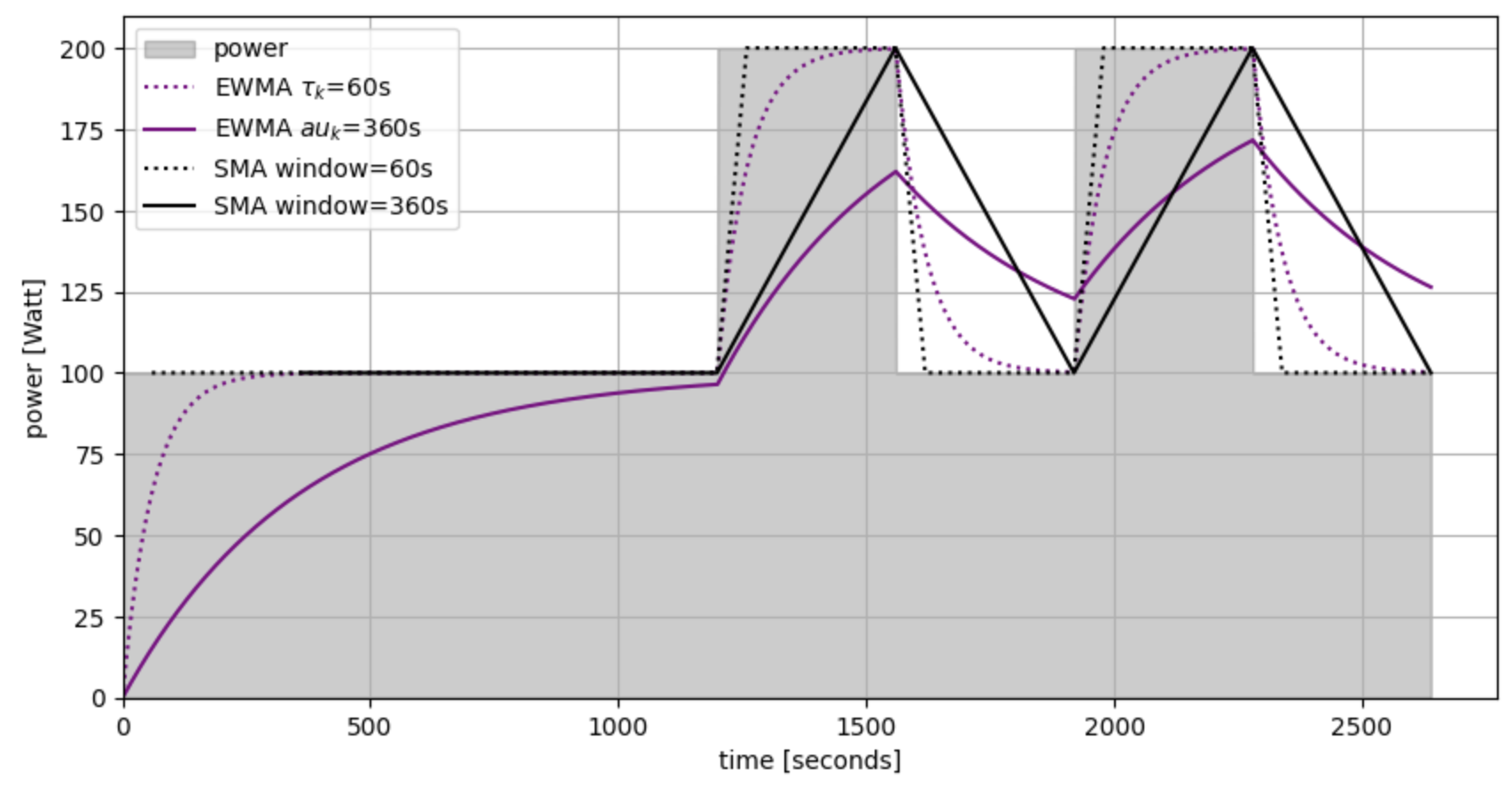
As you can see, the SMA “responds” much faster to the changes in power output, with the EWMA (\(\tau_k = 300s\)) not even nearly reaching the average power of the 6 minute intervals.

With a little experimenting, I came to the conclusion that the time-characteristic (\(\tau_k\)) of the EWMA that is used in the paper needs to be decreased quite a bit to better align with my expections and that (for example) calculating alpha from a “span” that is equal to the window used in the SMA calculation, yields results that align much better with my intuition.

$$ \alpha = \frac{2}{1 + \text{window}} $$

In Python/Pandas, this would look like this:

alpha = 2 / (1 + window)
ewma = power.ewm(alpha=alpha, adjust=False).mean()

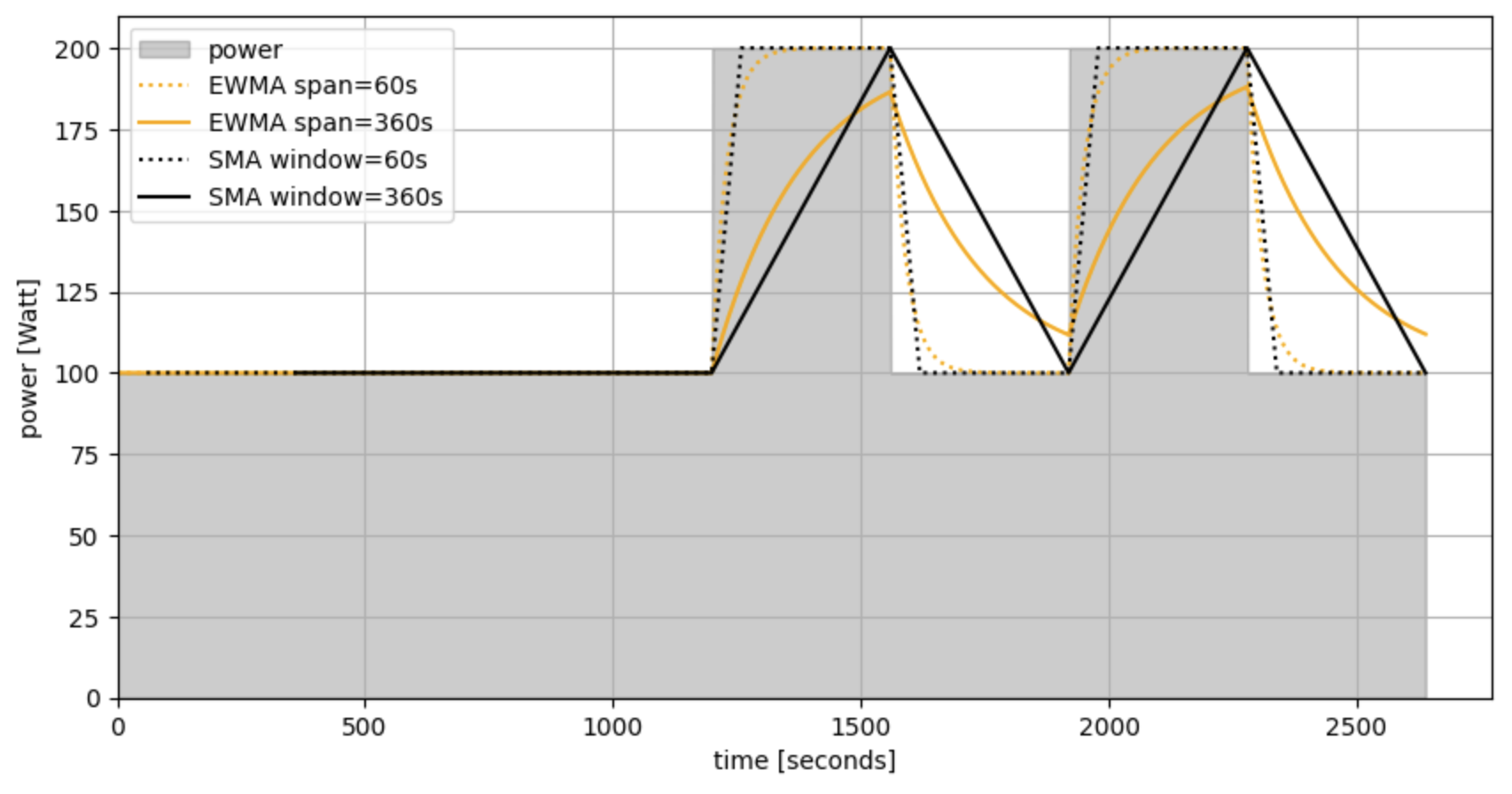
Finally, to be really clear about this: This is just an example of my intuition going for a walk and not a critique on the methods used in the paper or on using EWMA’s in general.